문제 설명
길이가 같은 배열 A, B 두개가 있습니다. 각 배열은 자연수로 이루어져 있습니다.
배열 A, B에서 각각 한 개의 숫자를 뽑아 두 수를 곱합니다. 이러한 과정을 배열의 길이만큼 반복하며, 두 수를 곱한 값을 누적하여 더합니다. 이때 최종적으로 누적된 값이 최소가 되도록 만드는 것이 목표입니다. (단, 각 배열에서 k번째 숫자를 뽑았다면 다음에 k번째 숫자는 다시 뽑을 수 없습니다.)
예를 들어 A = [1, 4, 2] , B = [5, 4, 4] 라면
A에서 첫번째 숫자인 1, B에서 첫번째 숫자인 5를 뽑아 곱하여 더합니다. (누적된 값 : 0 + 5(1x5) = 5)
A에서 두번째 숫자인 4, B에서 세번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 5 + 16(4x4) = 21)
A에서 세번째 숫자인 2, B에서 두번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 21 + 8(2x4) = 29)
즉, 이 경우가 최소가 되므로 29를 return 합니다.
배열 A, B가 주어질 때 최종적으로 누적된 최솟값을 return 하는 solution 함수를 완성해 주세요.
제한사항
배열 A, B의 크기 : 1,000 이하의 자연수
배열 A, B의 원소의 크기 : 1,000 이하의 자연수
입출력 예
| A | B | answer |
| [1, 4, 2] | [5, 4, 4] | 29 |
| [1,2] | [3,4] | 10 |
입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
A에서 첫번째 숫자인 1, B에서 두번째 숫자인 4를 뽑아 곱하여 더합니다. (누적된 값 : 4) 다음, A에서 두번째 숫자인 2, B에서 첫번째 숫자인 3을 뽑아 곱하여 더합니다. (누적된 값 : 4 + 6 = 10)
이 경우가 최소이므로 10을 return 합니다.
풀이 - 1
처음에는 문제가 잘 이해가 되지않았는데, 예제를 보고나니 A의 최소값과 B배열의 최대값을 곱하여 answer에 더해주는 방식이고, 사용한 숫자는 버리는 방식으로 진행하였다.
우선 A배열의 최소값과 B배열의 최대값을 곱하여 더해주고난뒤 A배열의 최소값 index를 구하여 최대값 초과인 1001로 변경하고 B배열도 마찬가지로 최대값 index를 구하여 최소값 미만인 -1로 변경하는 식으로 풀이하였다.
function solution(A,B){
let answer = 0;
let minIndex;
let maxIndex;
// 반복문
for (let i = 0; i < A.length; i++) {
// A배열의 최소값과 B배열의 최대값을 꺼내어 곱하고 answer에 더해준다.
answer += Math.min(...A) * Math.max(...B);
// 최소값의 인덱스를 찾아 1001로 변경한다.
minIndex = findIndex(A, Math.min(...A));
A[minIndex] = 1001;
// 최대값의 인덱스를 찾아 -1로 변경한다.
maxIndex = findIndex(B, Math.max(...B));
B[maxIndex] = -1;
}
return answer;
}
function findIndex(numbers, target) {
const find = (e) => e === target;
return numbers.findIndex(find);
}시간복잡도를 최소화 하려했지만 인덱스를 구하는 과정에서 O(n^2)이 되어 효율성 테스트에서 떨어지게 되었다...
풀이 - 2
위에서 원래 sort함수를 사용하려 했는데 시간복잡도상 불리할것 같아 사용하지 않았는데 다른방법이 우선적으로 생각나서 적용해보았다.
먼저 A배열을 오름차순, B배열을 내림차순으로 하여 각 맨처음 요소가 최소값, 최대값이 되게끔 만들어주고 같은방식으로 서로 곱하여 더해주었다.
function solution(A,B){
let answer = 0;
// A배열 오름차순
A.sort((a, b) => a - b);
// B배열 내림차순
B.sort((a, b) => b - a)
// 반복문
for (let i = 0; i < A.length; i++) {
// A배열요소와 B배열 요소 곱하고 answer에 더해준다.
answer += A[i] * B[i];
}
return answer;
}먼저 풀이했던 방법보다 불리할것 같다고 생각했으나 이번에 효율성테스트를 통과한것으로 보아 시간복잡도 상 O(n^2)보다 O(2log)가 더 낫다고 이해되었다.
다른 풀이 참고용
좀더 나은방법이 있는지 보던 중 reduce를 활용한 방법이 있어 참고겸 작성해본다.
function solution(A,B){
// A배열 오름차순
A.sort((a, b) => a - b);
// B배열 내림차순
B.sort((a, b) => b - a)
return A.reduce((total, val, idx) => total + val * B[idx], 0)
}효율성 테스트도 통과하면서 코드 시인성도 좋게 만드는 효과가 있는거 같아 작성했는데 효율성테스트 결과를 보았을때 풀이 2번보다 간소하게 속도가 떨어지는 것으로 보인다.
| for 문 | reduce |
 |
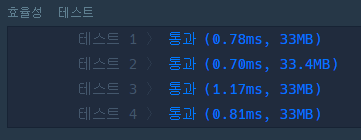 |
'개발일지 > TIL' 카테고리의 다른 글
| [프로그래머스] 이진 변환 반복하기 (0) | 2023.04.22 |
|---|---|
| [프로그래머스] 올바른 괄호 (0) | 2023.04.20 |
| [프로그래머스] JadenCase 문자열 만들기 (0) | 2023.04.19 |
| [Unity Devcamp] 0327 개발일지 (0) | 2023.03.28 |
| [Unity Devcamp] 0328 개발일지 (0) | 2023.03.28 |
